Boolsche Algebra

Einführung in die Boolsche Algebra

Die Boolsche Algebra ist ein Teilgebiet der Mathematik, das sich mit der Verarbeitung von Wahrheitswerten beschäftigt. Sie wurde von George Boole entwickelt und bildet die Grundlage der digitalen Schaltungstechnik sowie der Informatik. In der Boolschen Algebra gibt es nur zwei mögliche Werte: wahr (1) und falsch (0). Die grundlegenden Operationen sind:

UND (AND): Liefert nur dann 1, wenn beide Operanden 1 sind.

ODER (OR): Liefert 1, wenn mindestens einer der Operanden 1 ist.

NICHT (NOT): Invertiert den Wert, d. h., aus 1 wird 0 und aus 0 wird 1.

Die Boolsche Algebra wird häufig verwendet, um logische Ausdrücke zu beschreiben und in logische Schaltungen umzusetzen, wie beispielsweise in Computern, Steuerungssystemen und digitalen Geräten.

Aufgaben

Die Aufgaben werden mit Hilfe des Logic Gate Simulators bearbeitet.

Erstellen Sie eine Schaltung im Simulator, die zwei Eingangsvariablen verwendet und den AND-Operator implementiert. Überprüfen Sie, ob das Ergebnis nur dann wahr ist, wenn beide Eingänge wahr sind.

Schaltung erstellen

Es werden zwei Eingänge (Inputs) auf der Arbeitsfläche platziert.

Ein AND-Gatter wird auf die Arbeitsfläche gezogen.

Die beiden Eingänge werden mit den Eingängen des AND-Gatters verbunden.

Ein Ausgang (Output) wird platziert und mit der Ausgabe des AND-Gatters verbunden.

Testen

Die Eingangsvariablen werden auf verschiedene Kombinationen gesetzt und geprüft, on die Ausgabe nur bei (1,1) wahr ist:

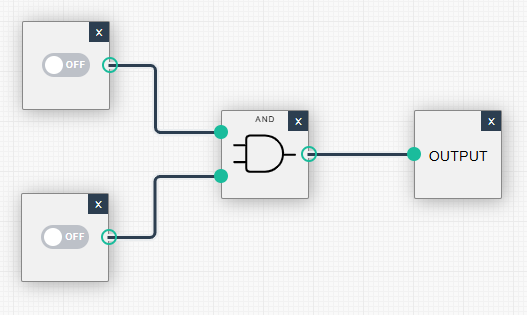
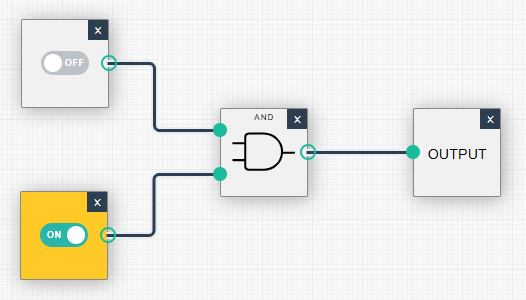
(0, 0): Ausgabe = 0	(0, 1): Ausgabe = 0

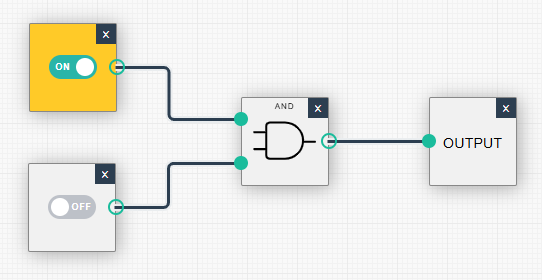
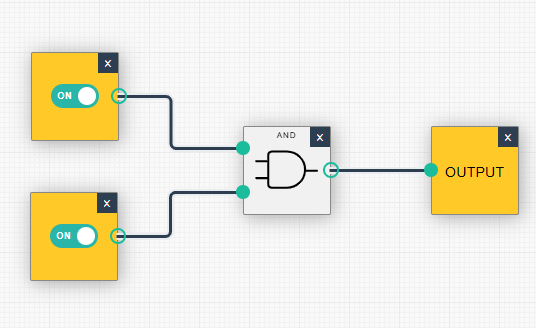
(1, 0): Ausgabe = 0	(1, 1): Ausgabe = 1

Modifizieren Sie die Schaltung, indem Sie einen NOT-Operator hinzufügen, um die Ausgabe des AND-Gatters zu invertieren. Beobachten Sie, wie sich das Ausgabesignal ändert.

Schaltung erweitern

Ein NOT-Gatter wird auf der Arbeitsfläche platziert.

Die Ausgabe des AND-Gatters wird mit dem Eingang des NOT-Gatters verbunden.

Die Ausgabe des NOT-Gatters wird mit dem Output verbunden.

Testen

Die Eingangsvariablen werden auf alle Kombinationen gesetzt. Es wird beobachtet, wie die Ausgabe invertiert wird:

(0, 0): Ausgabe = 1	(0, 1): Ausgabe = 1

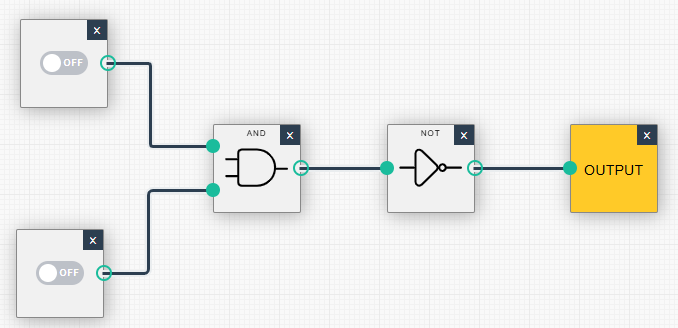
(1, 0): Ausgabe = 1	(1, 1): Ausgabe = 0

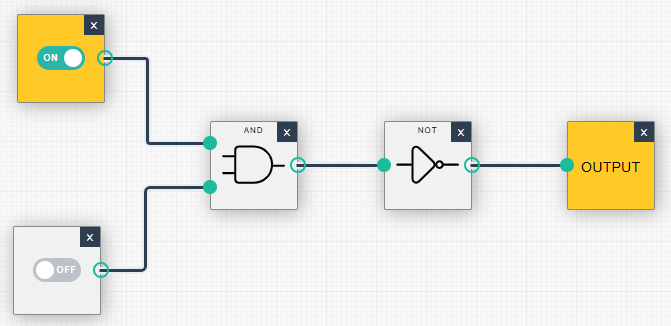
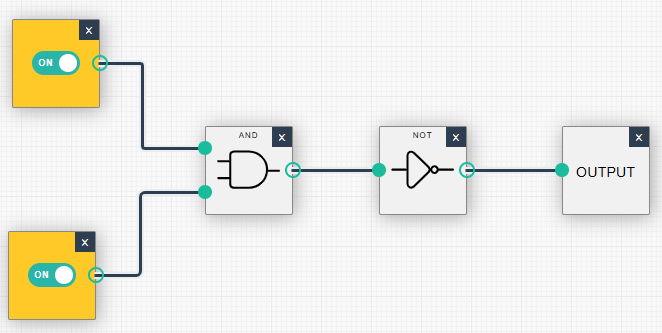
Konstruieren Sie eine Schaltung, die die OR-Operation zwischen zwei Variablen demonstriert. Testen Sie alle möglichen Kombinationen von Eingangswerten und notieren Sie die Ergebnisse.

Schaltung erstellen

Zwei Eingänge (Inputs) werden auf der Arbeitsfläche platziert.
Ein OR-Gatter wird auf die Arbeitsfläche gezogen.
Die Eingänge werden mit den Eingängen des OR-Gatters verbunden.
Die Ausgabe des OR-Gatters wird mit einem Output verbunden.

Testen

(0, 0): Ausgabe = 0	(0, 1): Ausgabe = 1

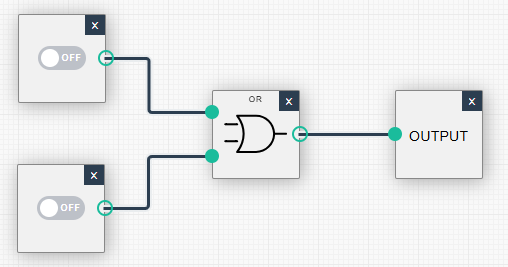
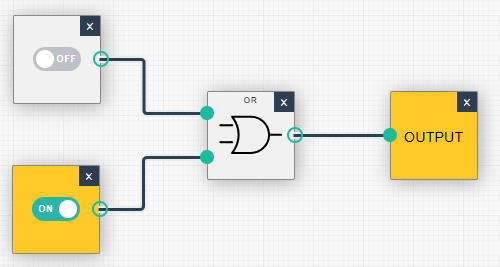
(1, 0): Ausgabe = 1	(1, 1): Ausgabe = 1

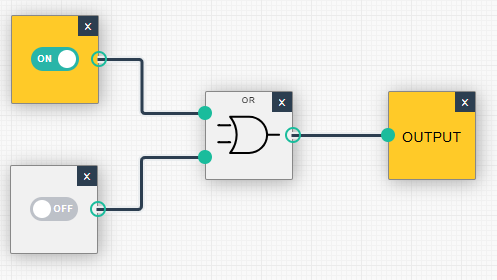
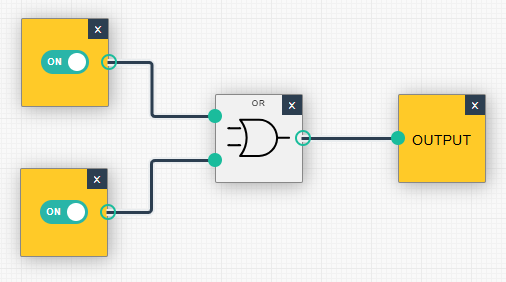
Erweitern Sie die Schaltung um eine Kombination aus AND, OR und NOT-Operatoren, um eine komplexere logische Funktion zu erstellen. Dokumentieren Sie Ihre Ergebnisse und erklären Sie, wie die Schaltung funktioniert.

Schaltungserweiterung

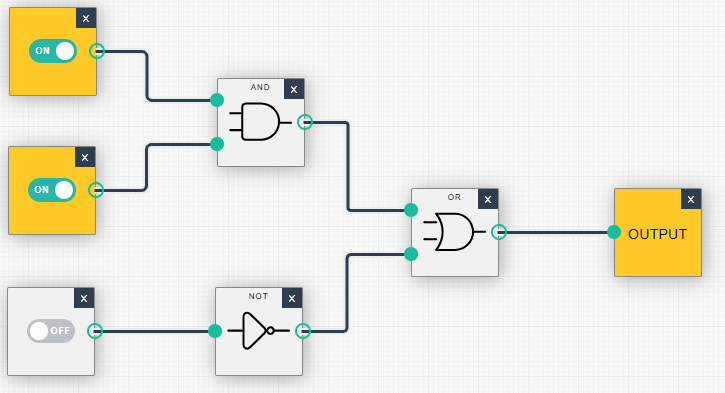
Eine Schaltung wird erstellt, die folgende logische Funktion umsetzt:

Output=(A AND B) OR (NOT(C))

Der Output ist wahr, wenn A und B beide wahr sind oder wenn C falsch ist.

Schaltung erstellen

Eingänge: Drei Eingänge (A, B und C) werden auf der Arbeitsfläche platziert.
AND-Gatter: A und B werden mit einem AND-Gatter verbunden.
NOT-Gatter: Der Eingang C wird mit einem NOT-Gatter verbunden.
OR-Gatter: Die Ausgaben des AND-Gatters und des NOT-Gatters werden mit einem OR-Gatter verbunden.
Output: Die Ausgabe des OR-Gatters wird mit einem Ausgang verbunden.

Testen

Die Eingangsvariablen werden auf alle möglichen Kombinationen von A, B und C gesetzt, und die Ergebnisse werden notiert.

(0, 0, 0): Ausgabe = 1	(0, 0, 1): Ausgabe = 0

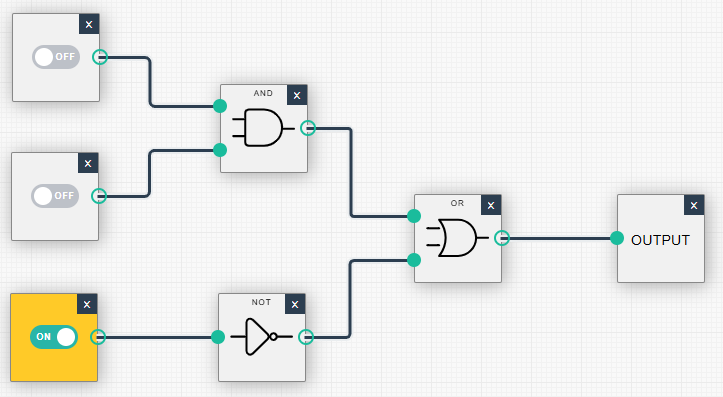
(0, 1, 0): Ausgabe = 1	(0, 1, 1): Ausgabe = 0

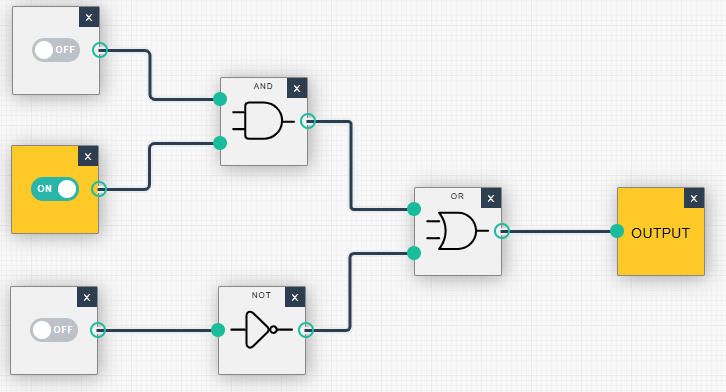
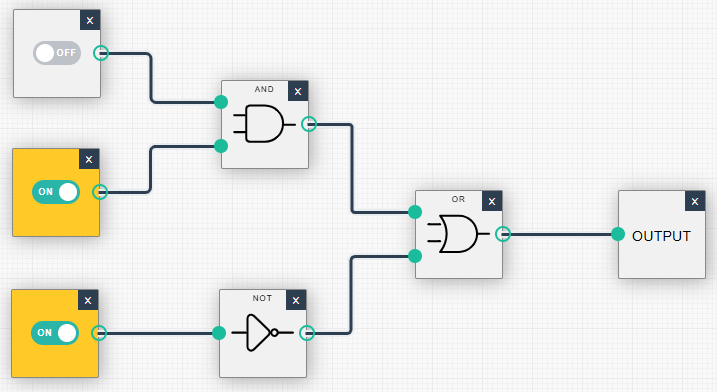
(1, 0, 0): Ausgabe = 1	(1, 0, 1): Ausgabe = 0

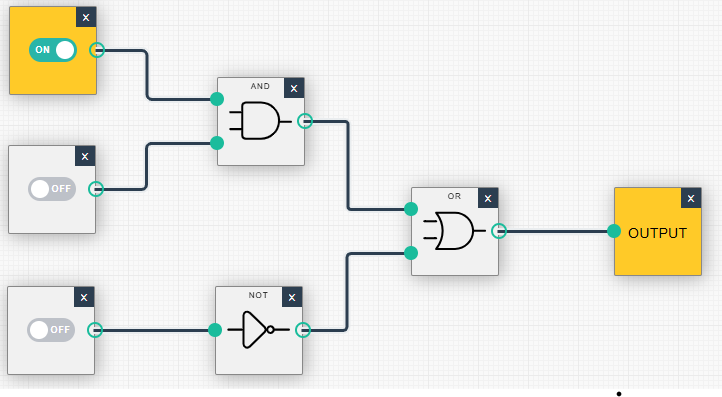
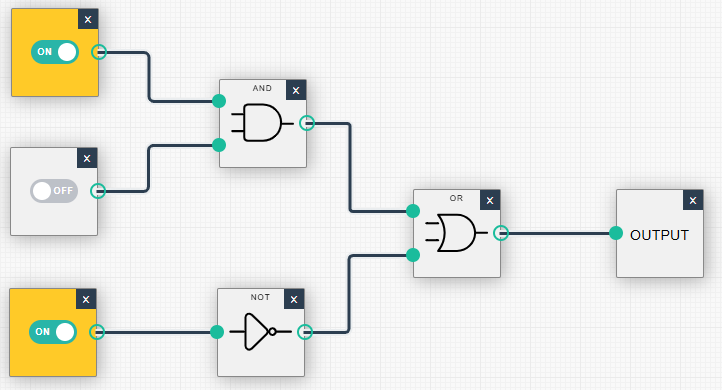
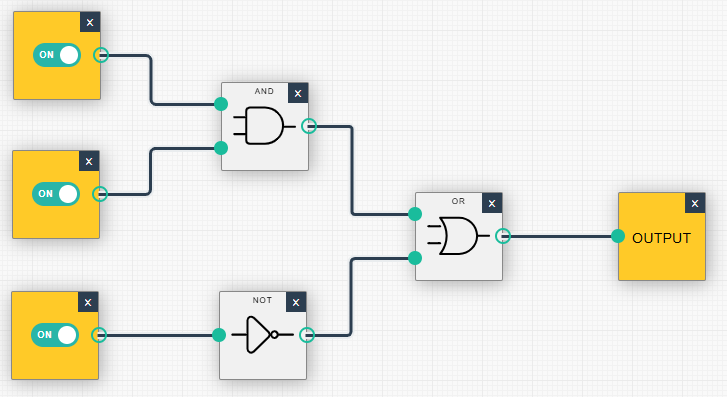
(1, 1, 0): Ausgabe = 1	(1, 1, 1): Ausgabe = 1

Funktionsweise

Das AND-Gatter überprüft, ob A und B beide wahr sind.

Das NOT-Gatter invertiert den Wert von C. Wenn C falsch ist (0), wird es wahr (1).

Das OR-Gatter kombiniert die Ergebnisse des AND- und NOT-Gatters.

Der Output ist wahr, wenn mindestens eine der Bedingungen erfüllt ist:

A AND B ist wahr.

C ist falsch (nach Invertierung durch das NOT-Gatter).

Einstein-Rätsel

Anwendung der Booleschen Algebra

In dieser Übung geht es darum, das berühmte Einstein-Rätsel zu lösen, indem man die Prinzipien der Booleschen Algebra anwendet. Ziel ist es, herauszufinden, wer welches Haustier hält, indem man logische Operatoren kombiniert und die Hinweise des Rätsels systematisch überprüft.

Wer hat den Fisch als Haustier?

Der Brite lebt im roten Haus.
Der Schwede hält einen Hund.
Der Däne trinkt gerne Tee.
Das grüne Haus steht links vom weißen Haus.
Der Besitzer des grünen Hauses trinkt Kaffee.
Die Person, die Poker spielt, hält einen Vogel.
Der Besitzer des gelben Hauses spielt Dart.
Die Person im mittleren Haus trinkt Milch.
Der Norweger wohnt im ersten Haus.
Der Mann, der Billard spielt, wohnt neben dem, der eine Katze hält.
Der Mann mit dem Pferd wohnt neben dem, der Dart spielt.
Der Hobby-Fußballer trinkt Bier.
Der Deutsche spielt Schach.
Der Norweger wohnt neben dem blauen Haus.
Der Mann, der Billard spielt, hat einen Nachbarn, der Wasser trinkt.

Schritt 1: Übersicht

Die Lösung basiert auf fünf Eigenschaften:

Nationalität (Brite, Schwede, Däne, Norweger, Deutscher)

Hausfarbe (rot, grün, weiß, gelb, blau)

Getränk (Tee, Kaffee, Milch, Bier, Wasser)

Haustier (Hund, Vogel, Katze, Pferd, Fisch)

Hobby (Poker, Dart, Billard, Fußball, Schach)

Schritt 2: Tabelle zur Lösung

Eine Tabelle wird mit den fünf Häusern erstellt, und die Eigenschaften werden gemäß den Hinweisen zugeordnet.

Haus-Nr	Nationalität	Farbe	Getränk	Haustier	Hobby
1	Norweger	gelb	Wasser	Katze	Dart
2	Däne	blau	Tee	Pferd	Billard
3	Brie	rot	Milch	Vogel	Poker
4	Deutscher	grün	Kaffee	Fisch	Schach
5	Schwede	weiß	Bier	Hund	Fußball

Schritt 3: Antwort

Der Deutsche, der im grünen Haus wohnt, hat den Fisch als Haustier.